- Išsiųsime per 10–14 d.d.
- Autorius: Peter Müller
- Leidėjas: Books on Demand
- Metai: 2011
- Puslapiai: 112
- ISBN-10: 3842380380
- ISBN-13: 9783842380387
- Formatas: 14.8 x 21 x 0.7 cm, minkšti viršeliai
- Kalba: Anglų
- Extra -15 % nuolaida šiai knygai su kodu: ENG15
Atsiliepimai
Aprašymas
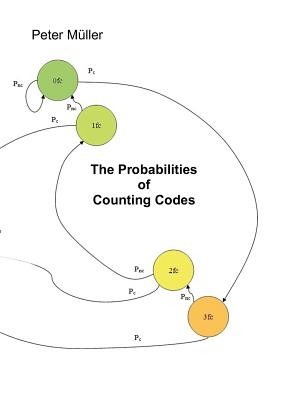
In many cases counters are used to count special events within an endless sequence of events. This paper discusses a specific calculation, related to the probability of a counter overrun if the special event occurs not in a predictable way but with a certain probability. Different counter codes are compared with each other. A probability formula is developed for special scenarios which are normally analyzed by state diagrams and which can be numerically solved by the related Markov chains. The target is to enable a non-numerical discussion of the topic. It is shown how formulas can be found based on the rules of the probability theory, and their correctness is verified by a comparison with Markov chains.EXTRA 15 % nuolaida su kodu: ENG15
Akcija baigiasi už 2d.04:42:53
Nuolaidos kodas galioja perkant nuo 10 €. Nuolaidos nesumuojamos.

- Autorius: Peter Müller
- Leidėjas: Books on Demand
- Metai: 2011
- Puslapiai: 112
- ISBN-10: 3842380380
- ISBN-13: 9783842380387
- Formatas: 14.8 x 21 x 0.7 cm, minkšti viršeliai
- Kalba: Anglų



Atsiliepimai